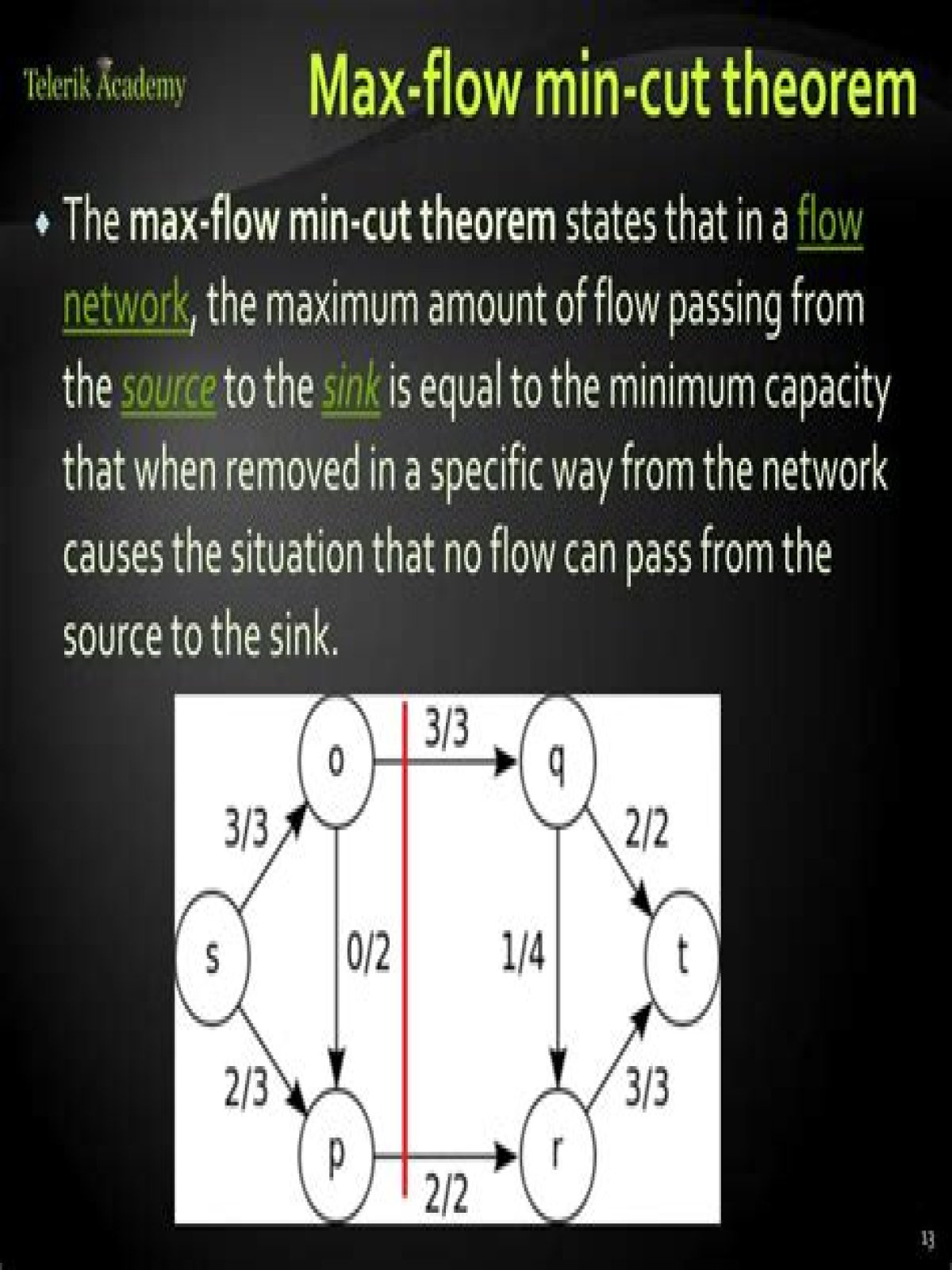
What does the max flow min cut theorem say?
The max-flow min-cut theorem states that the maximum flow through any network from a given source to a given sink is exactly equal to the minimum sum of a cut.
How do you prove max flow min cut theorem?
Proof of the Max-Flow/Min-Cut Theorem. We want to show that the 3 points of the theorem are equivalent, so we’ll prove that 1 =⇒ 2, 2 =⇒ 3 and 3 =⇒ 1. 1 =⇒ 2: Let f be a max flow and suppose Gf still has an augmenting path P. Then we can increase val(f) by augmenting along P, thus contradicting the maximality of f.
How do you calculate minimum cut?
1) Run Ford-Fulkerson algorithm and consider the final residual graph. 2) Find the set of vertices that are reachable from the source in the residual graph. 3) All edges which are from a reachable vertex to non-reachable vertex are minimum cut edges. Print all such edges.
What is Ford-Fulkerson theorem?
Ford-Fulkerson algorithm is a greedy approach for calculating the maximum possible flow in a network or a graph. A term, flow network, is used to describe a network of vertices and edges with a source (S) and a sink (T). Each vertex, except S and T, can receive and send an equal amount of stuff through it.
What is the maximum flow value?
The maximum value of an s-t flow (i.e., flow from source s to sink t) is equal to the minimum capacity of an s-t cut (i.e., cut severing s from t) in the network, as stated in the max-flow min-cut theorem.
What is Ford Fulkerson Theorem?
What is cut and Min cut?
In graph theory, a minimum cut or min-cut of a graph is a cut (a partition of the vertices of a graph into two disjoint subsets) that is minimal in some metric. Variations of the minimum cut problem consider weighted graphs, directed graphs, terminals, and partitioning the vertices into more than two sets.
Is Fulkerson an NP?
Yes, the Ford-Fulkerson algorithm is a pseudopolynomial time algorithm. Its runtime is O(Cm), where C is the sum of the capacities leaving the start node. Since writing out the number C requires O(log C) bits, this runtime is indeed pseudopolynomial but not actually polynomial.